
The trigonometric functions of sine, cosine, and tangent can be calculated using a unit circle. Trigonometric Functions using Unit Circle Let us now study the use of unit circles in trigonometry. The unit circle is considered as the so-called ideal boundary of the two-dimensional hyperbolic plane H 2 in both the Poincaré hyperbolic disk and Klein-Beltrami models of hyperbolic geometry.The unit circle can also be considered to be the contour in the complex plane defined by |x| = 1, where |x| represents the complex modulus.The unit circle has the ability to explicitly write the coordinates of a number of points lying on the unit circle with very little computation.The functions of trigonometry are most simply defined using the unit circle.Some of the areas where we find extensive use and application of unit circles include: The unit circle plays a significant role in a number of different areas of mathematics. But, the question arises that what is so peculiar about a unit circle and what is its importance in mathematics that we need to learn about it separately inline any other circle having a different centre and a radius. Now we have understood what a unit circle is. The centre of the unit circle is the point of origin, i.e.
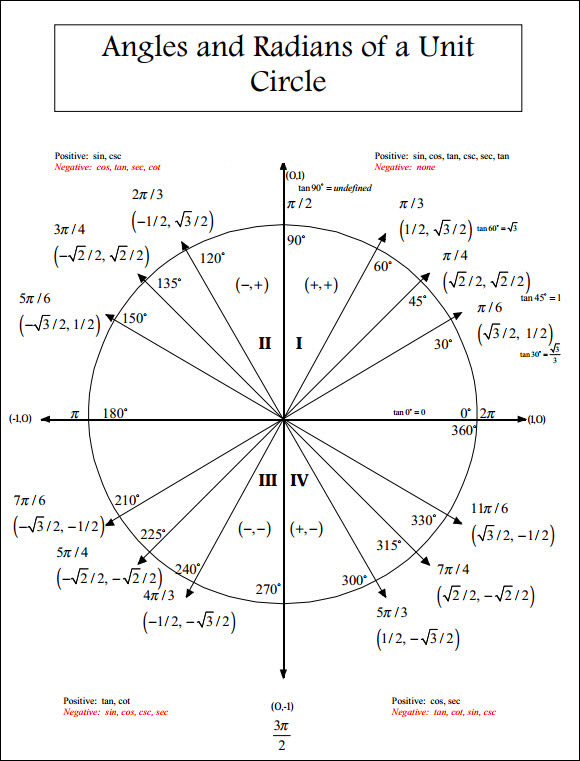
The centre of the unit circle just like its radius is a fixed point. Where does the centre of the unit circle lie? Can it be any point on the Cartesian Coordinate Plane or it is also fixed like the radius of the unit circle? We now know that by definition, the radius of the unit circle is always 1. Radius of the Unit Circleīy the very definition of the unit circle, it is clear that the radius of the unit circle is always one unit.
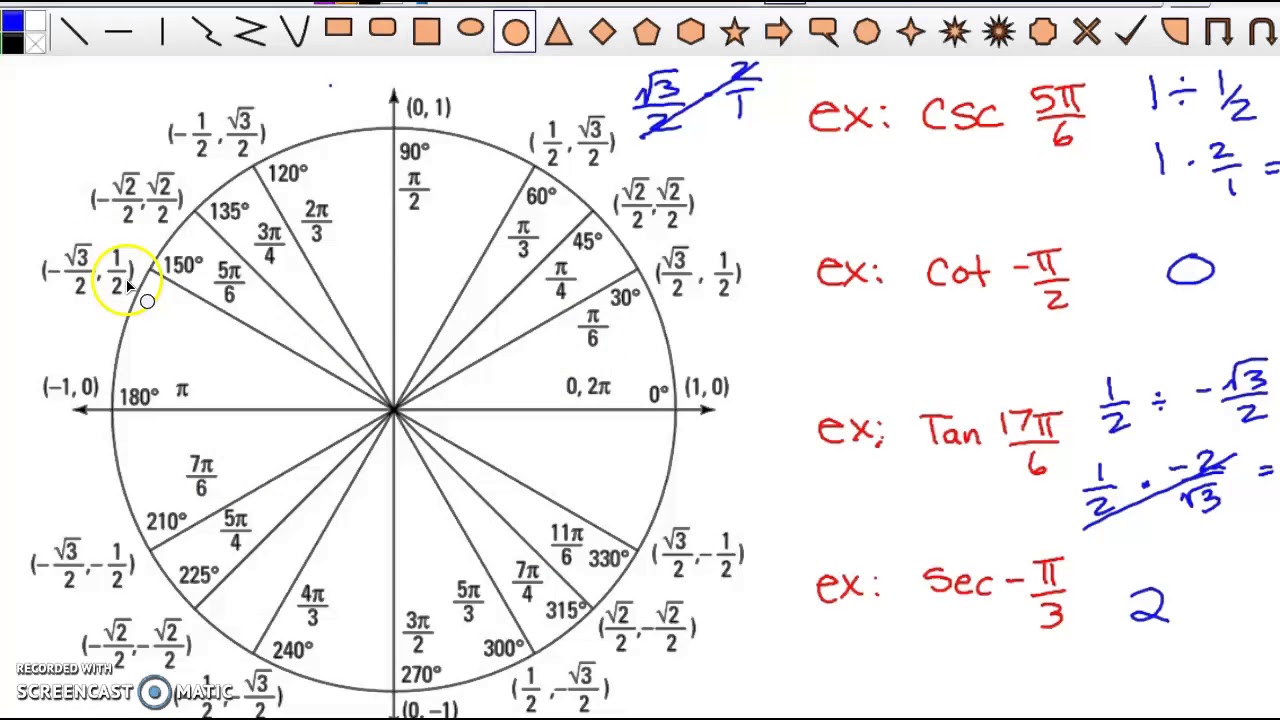
So, how do we define the values of the centre and the radius of the unit circle? Let us find out. We have learnt in the circle that that radius and the centre are two important components for studying circles. The following figure represents the circle with the radius as 1 unit. Therefore it can easily be made out that a unit circle is a circle with a radius of 1. The meaning of unit, as we all know is 1. Let us find out what do we mean by a unit circle? Definition: The curve formed by AQ is the arc of the circle.Ī type of circle is the unit circle. The line segment AQ is a chord of the circle that joins two points A and Q that lie on the boundary of the circle. Note that the line segment PQ is passing through the centre O The lone segment PQ is the diameter of the circle.
The line segment AO is the radius of the circle. In the circle above, O is the centre of the circle. The diameter is the longest chord of a circle. It is twice the length of the radius.Ĭhord of a Circle – The chord of a circle is the line from one point on the boundary of the circle to another point. Radius – Radius is the distance from the centre of a circle to any point on the boundary of the circle.ĭiameter – Diameter is the line from one point on the boundary of the circle to another point and passing through the centre of the circle. In other words, it is the perimeter of the circle. Parts of a CircleĬircumference – The circumference of a circle is the distance around the boundary of the circle.
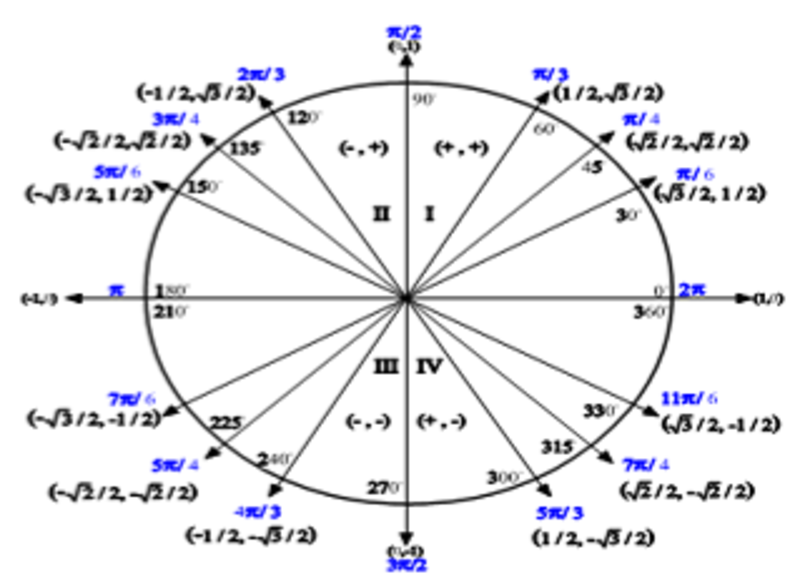
This fixed distance is called the radius of the circle and the fixed point is called the centre of the circle. It is a two-dimensional figure formed by a set of points that are at a constant or at a fixed distance from a fixed point in the plane. We have learnt that a circle is a type of shape. To study the unit circle and learn about its properties and importance in mathematics, let us first recall what a circle is. Trigonometric Functions using Unit Circle.Importance of Unit Circle in Mathematics.


 0 kommentar(er)
0 kommentar(er)
